So we have the following polynomial:
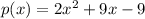
And we need to find p(3/4). We just need to replace x with 3/4:
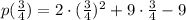
Remember that the power of a fraction meets the following:
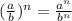
Then we have:
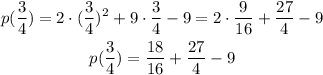
And we can rewrite 27/4 by multiplying and dividing it by 4 and we can multiply and divide 9 by 16:
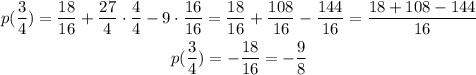
Then the answer is -9/8.