SOLUTION
Given that the money borrowed is $425 and the amount paid back each week thereafter is $30. Let A(n) be the amount paid back after n weeks. Since $30 is paid back to my friend after each week, so (n-1)30 is returned to my friend after (n-1) weeks. Also since I borrowed $425 in the first week, so the amount to return after (n) weeks is 425-(n-1)(30). Therefore, the sequence below represents the amount left to return after n weeks.
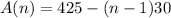
Hence, the sixth term in the context of this situation means the amount remaining for me to pay my friend after the 6th week, i.e, n=6.
The first six terms in the sequence can be derived by using the sequence formula defined above:
The first term will be when n =1
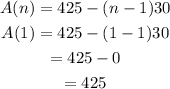
The second term will be when n =2
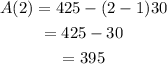
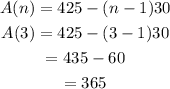
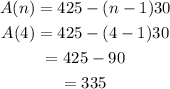
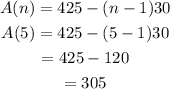
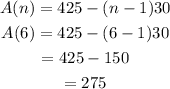
Hence, the first six terms are 425, 395,365,335,305,275 respectively.