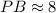Question

n the diagram below, if the lengths of the segments are AP = 5, PD = 8, and CP = 4, what is the length

Answer 1

Given:

`\begin{gathered} AP=5 \\ \\ PD=8 \\ \\ CP=4 \end{gathered}`

Find-:

The value of length PB

Explanation-:

The length of PB is:

When two chords intersect inside a circle, then the measures of the segments of each chord multiplied by each other are equal to the product from the other chord:

So, the value of PB is:

The applied property for the given circle is:

`AD\cdot PD=CB\cdot PB`

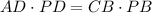
Then the value of PB is:

`PB=(AD\cdot PD)/(CB)`
`\begin{gathered} PB=((AP+PD)(PD))/(CB) \\ \\ PB=((5+8)(8))/(4+PB) \\ \\ PB(4+PB)=104 \\ \\ PB=8.3\text{ and }PB=-12.39 \end{gathered}`

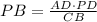
The length negative is not possible so, the value of PB is:

`PB\approx8`