An equation of a Proportional relationship has the following form:
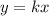
Where "k" is called Constant of proportionality.
The graph of Proportional relationships is a line that passes through the point (0,0), which is known as Origin.
For this case you have the first equation:
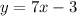
Notice that this an Equation of the line that is written in Slope-Intercept form, so its slope and y-intercept are:

Since the line does not pass through the origin, it is not a proportional relationship.
The second equation is:
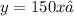
Notice that it has the form:
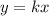
Whose Constant of proportionality (its slope), is:
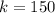
Therefore:
- The first equation does not represent a Proportional relationship.
- The second equation represents a Proportional relationship.