Question

Whats the equation of (-1,-1) and (2,8)

Answer 1

We have to find the equation of the line that pass through (-1,-1) and (2,8).

We can start by calculating the slope as:

`m=(y_2-y_1)/(x_2-x_1)=(8-(-1))/(2-(-1))=(9)/(3)=3`

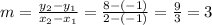
Then, we can take a point and the calculated slope and write the equation in slope-point form and then rearrange it:

`\begin{gathered} y-y_1=m(x-x_0) \\ y-8=3(x-2) \\ y=3x-3\cdot2+8 \\ y=3x-6+8 \\ y=3x+2 \end{gathered}`

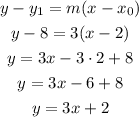
Answer: y = 3x+2