Question

In a race in which six automobiles are entered and there are no ties, in how many ways can the first three finishers come in? There are __ ways for the first three finishers to come in.

Answer 1

Given that: In a race in which six automobiles are entered and there are no ties

To Determine: In how many ways can the first three finishers come in?

Solution:

This question can be solved using the permutations formula. If there are a total of n objects and r of these objects have to be ordered, the number of ways doing so is

`^nP_r=(n!)/((n-r)!)`

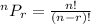
The number of automobiles is 6. This is the number of objects out of 3 that have to be ordered. So, n=6 and r=3.

The number of ways in which the race can finish will be:

`^6P_3=(6!)/((6-3)!)`
`\begin{gathered} ^6P_3=(6!)/(3!) \\ ^6P_3=(6*5*4*3!)/(3!) \\ ^6P_3=(6*5*4)/(1) \\ ^6P_3=120 \end{gathered}`

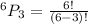
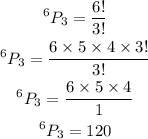
Hence, there are 120 ways for the first three finishers to come in