Question

Quadrialteral GEOM is dilated by a scale factor of 2 centered at (0,0) to create quadrilateral GEOM select all the statements that are true about the dilation

Answer 1

To answer this question, we need have to dilate the quadrilateral GEOM by a factor of 2 centered at (0,0). The rule for this is as follows:

`(x,y)\rightarrow(2x,2y)`

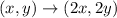
Then, from the graph above, we can identify each of the vertices of the quadrilateral as follows:

`E(0,0),O(-2,-1),M(-3,3),G(-1,3)`

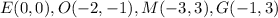
If we follow the rule for the dilation by 2 centered at (0,0), we have:

`E^(\prime)\rightarrow E(0,0)\rightarrow E^(\prime)(2\cdot0,2\cdot0)\rightarrow E^(\prime)(0,0)`
`O^(\prime)\rightarrow O(-2,-1)\rightarrow O^(\prime)(2\cdot(-2),2\cdot(-1))\rightarrow O^(\prime)(-4,-2)`
`M^(\prime)\rightarrow M(-3,3)\rightarrow M^(\prime)(2\cdot(-3),2\cdot(3))\rightarrow M^(\prime)(-6,6)`
`G^(\prime)\rightarrow G(-1,3)\rightarrow G^(\prime)(2\cdot(-1),2\cdot(3))\rightarrow G^(\prime)(-2,6)`

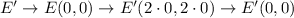
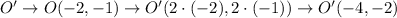
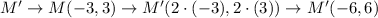
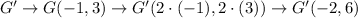
Now, we have that the image of the quadrilateral is given by the coordinates:

`E^(\prime)O^(\prime)M^(\prime)G^(\prime)=(0,0),(-4,-2),(-6,6),(-2,6)`

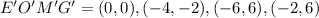
If we graph both quadrilaterals, the preimage EOMG, and the image E'O'M'G', we have:

Then, we can say that:

First Statement

`\bar{EO}\cong\bar{E^(\prime)O^(\prime)}\Rightarrow False`

E'O' is twice larger than EO.

Second Statement

`M^(\prime)G^(\prime)=2MG\Rightarrow True`

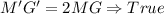
We can check using the x-coordinates in either case:

`MG=-1-(-3)=-1+3=2`
`M^(\prime)G^(\prime)=-2-(-6)=-2+6=4`
`M^(\prime)G^(\prime)=4=2\cdot MG=2\cdot2=4`

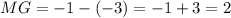
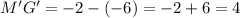
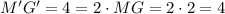
Third Statement

The segment M'G' will overlap the segment MG ---> False. We can see that this is not true: both segments have different positions at x- and y-values (see the graph above).

Fourth Statement

The segment E'O' will overlap the segment EO ---> False. If we speak in a strict way, we can say that the segment EO overlaps the segment E'O'.

Fifth Statement

The slope of the segment MO is equal to the slope of the segment M'O' ---> True. We can check this using the slope formula in each case:

MO ---> (-3,3) (-2,-1) ---> x1 = -3, y1 = 3, x2 = -2, y2 = -1

M'O' ---> (-6,6) (-4, -2) ---> x1 = -6, y1 = 6, x2 = - 4, y2 = -2

`m_(MO)=(y_2-y_1)/(x_2-x_1)=\frac{-1-3}{-2-(-3)_{}}=(-4)/(-2+3)=-(4)/(1)=-4`
`m_(M^(\prime)O^(\prime))=(-2-(6))/(-4-(-6))=(-2-6)/(-4+6)=(-8)/(2)=-4`

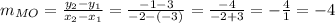
Then, both slopes are equal.

In summary, we have:

First Statement

`\bar{EO}\cong\bar{E^(\prime)O^(\prime)}\Rightarrow False`

Second Statement

`M^(\prime)G^(\prime)=2MG\Rightarrow True`

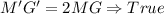
Third Statement

The segment M'G' will overlap the segment MG ---> False.

Fourth Statement

The segment E'O' will overlap the segment EO ---> False. If we speak in a strict way, we can say that the segment EO overlaps the segment E'O' (please, check this with your teacher). If the case is the second one, the answer is True. (Overlap is "cover part, extend over so as to cover partly.")

Fifth Statement

The slope of the segment MO is equal to the slope of the segment M'O' ---> True.