Question

If an island's only residents are penguins and bears, and if there are 19 heads and 44 feet on the island, how many penguins and how many bearsare on the island?

Answer 1

Okay, here we have this:

Considering the provided information, we are going to calculate the number of each animal, so we obtain the following:

Let's first consider that each penguin and bear have only one head, and each penguin has 2 feet, and each bear has 4 feet, then we have the following system of equations:

`\begin{bmatrix}x+y=19 \\ 2x+4y=44\end{bmatrix}`

Where x represents the number of penguins and the number of bears, then we will solve the system:

First we isolate x in the first equation:

`x=19-y`

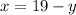
And we replace with this in the second equation:

`\begin{gathered} \begin{bmatrix}2\mleft(19-y\mright)+4y=44\end{bmatrix} \\ 38-2y+4y=44 \\ \begin{bmatrix}38+2y=44\end{bmatrix} \end{gathered}`

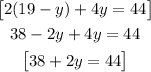
Solving for y:

`\begin{gathered} 38+2y-38=44-38 \\ 2y=6 \\ y=3 \end{gathered}`

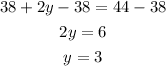
Finally we replace with this value in the first equation of x:

`\begin{gathered} x=19-y \\ x=19-3 \\ x=16 \end{gathered}`

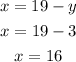
Finally we get that there are 16 penguins and 3 bears.