First, notice that since the sum of the internal angles of any triangle must always be equal to 180, then:
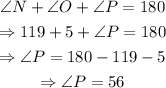
Draw a diagram of the triangle to visualize the situation:
Draw the altitude of the triangle through the vertex N. Let H be the point where the altitude through N intercepts the line OP. From the trigonometric relations, notice the following:
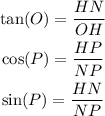
Substitute the known values:
![\begin{gathered} \tan (5)=(h)/(OH) \\ \cos (56)=\frac{HP}{3.6\operatorname{cm}} \\ \sin (56)=\frac{h}{3.6\operatorname{cm}} \end{gathered}]()
Isolate OH from the first equation, HP from the second and h from the third one:
![\begin{gathered} OH=(h)/(\tan (5)) \\ HP=3.6\operatorname{cm}*\cos (56) \\ h=3.6\operatorname{cm}*\sin (56) \end{gathered}]()
Substitute the expression for h from the third equation into the expression for OH:
![OH=\frac{3.6\operatorname{cm}*\sin (56)}{\tan (5)}]()
Finally, notice that the length of n equals the length of the segment OP, which is the sum of the lengths of the segments OH and HP:
![\begin{gathered} n=OH+HP \\ =3.6\operatorname{cm}*(\sin(56))/(\tan(5))+3.6\operatorname{cm}*\cos (56) \\ =34.1134\ldots cm+2.0131\ldots cm \\ =36.1265\ldots cm \end{gathered}]()
Therefore, to the nearest tenth:
![n=36.1\operatorname{cm}]()