The complete table would be the follwing:
A.
To get this probability, we take the total number people who pefer an SUV, and divide it by the total number of people in the sample
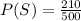
B.
To get this probability, we take the total number of females, and divide it by the total number of people in the sample

C.
To get this probability, we take the total number of females who pefer a car, and divide it by the total number of people in the sample
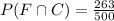
D.
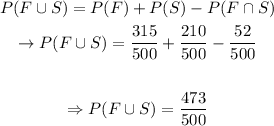
E.
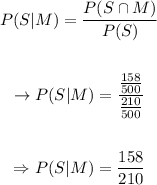
F.

In the final question we're being asked for:
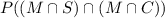
This is:
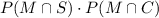
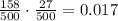
Therefore, this probability is 0.017