The equation of a line in point-slope form is:

Any point that belongs to this line is a solution to this equation. Looking at the graph we can see two points that belong to the line:
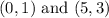
By replacing x and y in the equation of the line with the values given by the points we can build two equations:
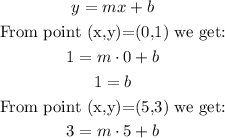
So we have these two equations:
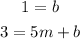
So according to the first equation b=1. If we replace this value in the second equation we can also find m:
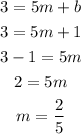
Then the equation of the line that we are looking for and the answer to this question is:
