Here we have to use the trigonometric formula for right-angled triangle.
This is the structure described in the question. We have to find x which is the angle between the wire and the ground.
From the trigonometric formula of right angled triangle we know that
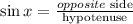
So
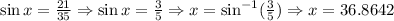
At the top of the pole the wire will make angle with the pole is
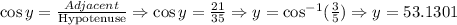
So the wire makes a 53.1301-degree angles with the top of the pole.