ANSWER
C) F/2
Step-by-step explanation
By the Coulomb's Law we know that the force between two charged particles is:
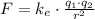
Where r is the distance between the particles, q1 and q2 are the charges and ke is Coulomb's constant.
Now, it is given that the distance between the particles is doubled. Let's call this new distance d:

And one of the particles now has double as charge as before. Let's say that this is the case of particle 1:
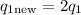
The force in this case is:
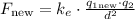
If we replace with the second and third equations:

Note that what's on the right is the force we initially had for the particles:
