Given
A cosine function has an amplitude of 2, a midline of 5 and a period of 8.
To find:
A cosine function.
Step-by-step explanation:
Let the function be,
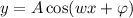
Since amplitude is 2.
Then,
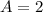
Also, since the period is 8.
Then,
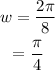
And, since midline is 5.
Then,
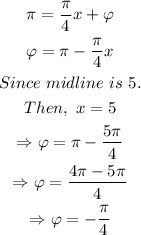
Hence, the cosine function is,
