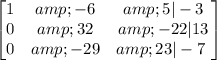The given matrix is:
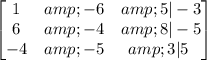
Each term in the matrix is the argument of a system of equations in the form:
ax+by+cz=d
Where a, b, c and d, are the elements in each row of the matrix. Then, the system of equations is:

And by simplifying it we obtain:
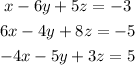
The answer is option D.
b. The row operations are:

Let's start with the first operation to find R2:
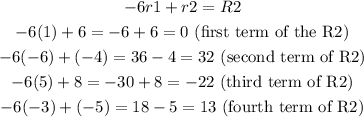
Now, for R3 we have:

Then, the resulting matrix is: