Question

Decide if the two trigonometric functions areequal. Choose Yes or No.

Answer 1

A. Yes

B. No

Step-by-step explanation:

A. Recall the below rules;

`\begin{gathered} \cos(-x)=\cos x \\ \sin x=\cos((\pi)/(2)-x) \end{gathered}`

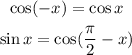
We'll go ahead and apply the above rules to simplify the given trig. functions as seen below;

`\sin(23\pi)/(3)=\cos((\pi)/(2)-(23\pi)/(3))=\cos(-(43\pi)/(6))=\cos((43\pi)/(6))=\cos((7\pi)/(6))=-(√(3))/(2)`
`\cos(-17\pi)/(6)=\cos(17\pi)/(6)=\cos(5\pi)/(6)=-(√(3))/(2)`

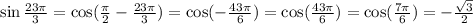
We can see that both trig functions are equal so we'll choose Yes.

B.

Let's go ahead and simplify the given trig functions as seen below;

`\tan(13\pi)/(4)=\tan(\pi)/(4)=1`
`\begin{gathered} Recall\text{ that }\tan(-x)=-\tan(x) \\ \tan(-13\pi)/(4)=-\tan(13\pi)/(4)=-\tan(\pi)/(4)=-1 \end{gathered}`

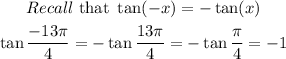
We can see that the two trig functions are not equal, so we'll choose No.