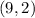Question

Which point is a solution to the inequality2x - 3y ≥ 12

Answer 1

Given:

`2x-3y\ge12`

Add 3y-12 to both sides of the inequality, we get

`2x-3y+3y-12\ge12+3y-12`

`2x-12\ge3y`

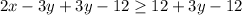
Dividing both sides by 3, we get

`(2x-12)/(3)\ge(3y)/(3)`

`(2x-12)/(3)\ge y`

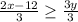
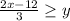
Let x=9 and substitute in this inequality, we get

`(2(9)-12)/(3)\ge y`

`(18-12)/(3)\ge y`

`(6)/(3)\ge y`

`2\ge y`

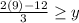
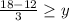
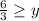
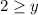
We get 2 is greater than or equal to y.

y values are 2,1,0,...

Hence the solutions to the given inequality are

`(9,2),(9,1),(9,0)`

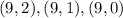
We need to check all the given options.

`(4,2)`

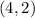
Substitute x=4 and y=2 in the inequality, we get

`2(4)-3(2)\ge12`

`2\ge12`

This is not true.

`(2,5)`

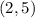
Substitute x=2 and y=5 in the inequality, we get

`2(2)-3(5)\ge12`

`-11\ge12`

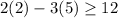
This is not true.

`(1,1)`

Substitute x=1 and y=1 in the inequality, we get

`2(1)-3(1)\ge12`

`-1\ge12`

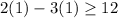
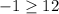
Hence the solution is

`(9,2)`