Question

Hi, how do i solve this? i know it’s a 30/60/90 triangle but i am confused

Answer 1

a) 5

b) 10

c) 5

d) 5√3

Step-by-step explanation:

From the left triangle:

hypotenuse = 5√2

opposite = a

adjacent = c

angle = 45°

To get a, we will use sine ratio:

`\begin{gathered} \sin \text{ 45}\degree\text{ = }(opposite)/(hypotenuse) \\ \sin \text{ 45}\degree\text{ = }\frac{a}{5\sqrt[]{2}} \\ 5\sqrt[]{2}\text{ (sin45}\degree)=a_{} \\ 5\sqrt[]{2}\text{ }*\text{(}\frac{\sqrt[]{2}}{2})\text{ = a} \\ (5(2))/(2)\text{ = a} \\ a\text{ = 5} \end{gathered}`

To get c, we will use cosine ratio:

`\begin{gathered} \cos \text{ 45}\degree\text{ = }\frac{adjacent}{\text{hypotenuse}} \\ \cos 45\degree\text{ = }\frac{c}{5\sqrt[]{2}} \\ 5\sqrt[]{2}\text{ (cos 45}\degree)\text{ = c} \\ 5\sqrt[]{2}\text{ (}\frac{\sqrt[]{2}}{2})\text{ = c} \\ (5(2))/(2)\text{ = c} \\ c\text{ = 5} \end{gathered}`

From right triangle:

angle = 30°

To get b, we will apply sine ratio:

`\begin{gathered} \sin \text{ 30}\degree\text{ = }\frac{opposite}{\text{hypotenuse}} \\ \sin \text{ 30}\degree\text{ = }(a)/(b) \\ \sin \text{ 30}\degree\text{ = }(5)/(b) \\ b(\sin \text{ 30}\degree\text{) = 5} \\ b((1)/(2))\text{ = 5} \\ b\text{ = 2(5) } \\ b\text{ = 10} \end{gathered}`

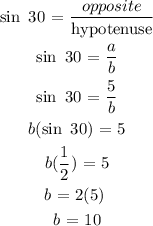
To get d, we will apply cosine ratio:

`\begin{gathered} \cos \text{ 30}\degree\text{ = }\frac{adjacent}{\text{hypotenuse}} \\ \cos \text{ 30}\degree\text{ = }(d)/(b) \\ \cos \text{ 30}\degree\text{ = }(d)/(10) \\ 10(\cos \text{ 30}\degree)\text{ = d} \\ 10*\frac{\sqrt[]{3}}{2}\text{ = d} \\ d\text{ = 5}\sqrt[]{3} \end{gathered}`