The diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circumference of the circle. The radius is half of the diameter. Then, we need to find the distance from point
(-5,0) to (-1,2).
The distance formula is given by
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
where
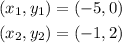
By substituying these values into the distance formula, we obtain
![d=\sqrt[]{(-1-(-5))^2+(2-0)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/hsldvxv7rh0azp5gdtfotemi5ran4ofsyu.png)
which gives
![\begin{gathered} d=\sqrt[]{4^2+2^2} \\ d=\sqrt[]{16+4} \\ d=\sqrt[]{20} \\ d=\sqrt[]{4\cdot5} \\ d=2\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3k52m3f0eeksu4sygh4ozxfjigghw56xep.png)
Finally, the lenght of the radius R is
![\begin{gathered} R=(d)/(2) \\ R=\frac{2\sqrt[]{5}}{2} \\ R=\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6d2nsyyxrzauikp5jizsn2fuyhm42uyth8.png)