We have to find the amplitude (A), period (P) and phase shift (PS) of the function:
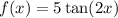
The amplitude for this function will be equal to the coefficient that multiplies the pure tangent function. In this case, the amplitude is A = 5.
The period is related to the coefficient inside the argument multiplying x: B = 2.
We can relate them as:
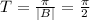
In this case, as there is no independent term inside the argument of the tangent function, there is no phase shift.
Also, there is no independent term outside the argument, so neither is a vertical shift.
Answer: A = 5, P = π/2, PS = (0,0) [Fourth option]