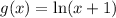Question

Give an equation for a logarithmic function that has the following features.The range of the function is (−∞, ∞).The domain of the function is (−1, ∞).The vertical asymptote of the function is x=−1.The graph crosses through the origin.

Answer 1

We must write a logarithmic function with the following properties:

0. The range of the function is (−∞, ∞).

,

1. The domain of the function is (−1, ∞).

,

2. The vertical asymptote of the function is x = −1.

,

3. The graph crosses through the origin.

To answer this question, first, we remember the parent logarithm function:

`f(x)=\ln x,`

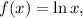
which has

• range = (−∞, ∞),

,

• domain = (0, ∞),

,

• vertical asymptote at x = 0,

,

• the value f(1) = 0.

Now, if we change the function in the following way:

`g(x)=\ln (x+1)\text{.}`

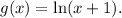
We see that now we have:

• range = (−∞, ∞),

,

• domain = (-1, ∞),

,

• vertical asymptote at x = -1,

,

• the value g(0) = 0 → the graph crosses through the origin.

Answer

`g(x)=\ln (x+1)`