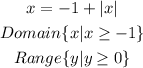From the given problem, we have two relations:
A)
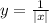
B)
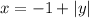
For the first relation (A), we know that x can be any number but 0 because a division by 0 is not defined. From this, we can say its domain will be all real numbers, but 0. And it is also possible to say that because of the module function, all values of y will be positive.
From the given statement, we conclude that the Domain and Range of the first relation are:
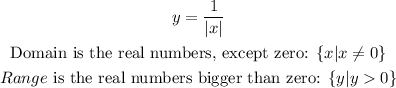
For the second relation, we need to isolate y to find the domain and range of it. To do so, we need to work with the modulus as follows:
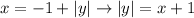
Now, because |y| is always a positive value, x can only assume values in which |y| ≥ 0, from this we can get:
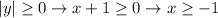
From this, we conclude the domains are the real numbers bigger than -1. And because it is a relationship where we know x will be increasing and y will follow it for all the values, with x always attending the restriction given above, we conclude the domain and range of the second relation are: