To be able to determine the equation of the line, we need to have a y-intercept and its slope.
The y-intercept is the value of y when x = 0. In the table that we have, when x = 0, g(x) = 5, hence, our y-intercept is 5.
Next, let's determine the slope. To determine the slope, we need two points and the formula below:
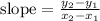
Let's make use of the points (0, 5) and (5, -10). These will be our (x₁, y₁) and (x₂, y₂). Let's plug these values to the slope formula above.

Hence, the slope of the line is -3.
Now that we have slope = -3 and y-intercept = 5, we can now use the slope-intercept equation of the line that is:

where m = slope and b = y-intercept.

Answer: The equation of the line is g(x) = -3x + 5.
Note that g(x) = y.