Question

Describe a similarity transformation that maps triangle ABC to triangle RST A(1,0), B(-2,-1) C(-1,-2) and R(-3,0) S(6,-3) T(3,-6) Fill in the blanks.

Answer 1

Given the vertices of triangles ABC and RST:

A(1, 0), B(-2, -1), C(-1, -2) and R(-3, 0), S(6, -3), T(3, -6)

Let's describe a transformation that maps triangle ABC to triangle RST.

The first form of transformation will be reflect triangle ABC over the line, x = -1.

Reflection over the line x = -1 is a reflection over the y-axis.

After a reflection over the y-axis, using the rules of reflection, we have:

(x, y) ==> (-x, y)

The next form of transformation will be a dilation with center (-3, 0).

To find the scale factor of dilation, let's divide the length of AB by the length of RS.

To find the length, use the distance formula:

`d=\sqrt[]{(x2-x1)^2+(y2-y1)^2}`

• Length of AB.

Given:

(x1, y1) ==> (1, 0)

(x2, y2) ==> (-2, -1)

`\begin{gathered} AB=\sqrt[]{(-2-1)^2+(-1-0)^2} \\ AB=\sqrt[]{9+1} \\ AB=\sqrt[]{10} \\ AB=3.16 \end{gathered}`

• Length of RS.

Given:

(x1, y1) ==> (-3, 0)

(x2, y2) ==> (6, -3)

`\begin{gathered} RS=\sqrt[]{(6-(-3))^2+(-3-0)^2} \\ RS=\sqrt[]{(6+3)^2+(-3)^2} \\ RS=\sqrt[]{81+9} \\ RS=\sqrt[]{90} \\ RS=9.48 \end{gathered}`

Now, to find the scale factor, we have:

`\begin{gathered} k=(RS)/(AB)=(9.48)/(3.16) \\ \\ k=3 \end{gathered}`

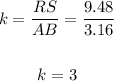
Therefore, the sacle factor of the dilation is 3.

This is triangle ABC above.

This is triangle RST

You can see triangle ABC is smaller than triangle RST.

ANSWER:

One way to map triangle ABC to RST is a relection in the line x = -1, followed by a dilation with center (-3, 0) with a scale factor k = 3.