Given the expression:
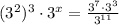
notice that on the left side, if we simplify, we have the following:
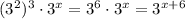
and on the right side, we have:
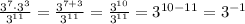
then, if we equate both expression we have that:
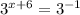
then, this must mean that the exponents are equal. This means the following:
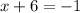
solving for x we get:
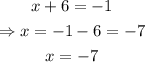
therefore, x = -7