To solve a system of equations using the substitution method
We use one equation to find x in terms of y, then
Substitute x in the second equation by the result of the first step
Since the given system is
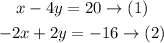
We will add equation (1) by 4y (each side) to find x in terms of y
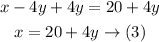
Now, substitute x in equation (2) by equation (3)
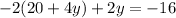
Simplify the left side
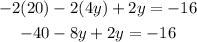
Add the like terms on the left side
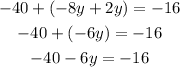
Add 40 to each side
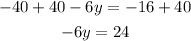
Divide both sides by -6 to find y
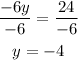
Substitute y in equation (3) by -4
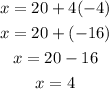
The answer is (x, y) = (4, -4)
x = 4
y = -4