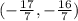We have the following system of equations:
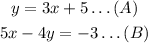
Solving by substituting method.
By substituting equation (A) into (B), we have
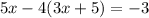
now, by distributing the number 4 into the panrentheses, we get

By combining similar terms, we obtain
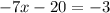
Now, by adding 20 to both sides, we have
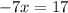
and by dividing both sides by -7, we get
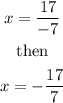
Once we know the result for x, we can subtitute that value into equation (A) and get
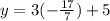
which gives
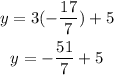
or equivalently,
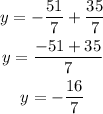
Therefore, the solution of the given system is:
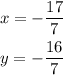
In order pair notation (x,y), the answer is expressed as: