Question

A ball is thrown upwards with an initial velocity of 6.1 m/s. What is the maximum height the ball will reach?

Answer 1

`\begin{equation*} 1.90\text{ m} \end{equation*}`

Step-by-step explanation

The maximum height of the ball occurs when the final velocity of the ball is 0 m/s.

Since the ball is thrown upwards, its acceleration is the acceleration due to gravity.

To find the maximum height reached by the ball, apply one of Newton's equations of motion:

`v^2=u^2-2gs`

where s = vertical distance traveled

v = final velocity

u = initial velocity

Note: -g is used instead of a since the acceleration, a, is the acceleration due to gravity in the negative(upward) direction.

Therefore, solving for s in the equation above:

`\begin{gathered} 0^2=6.1^2-2*9.8*s \\ \\ 19.6s=6.1^2=37.21 \\ \\ s=(37.21)/(19.6) \\ \\ s=1.90\text{ m} \end{gathered}`

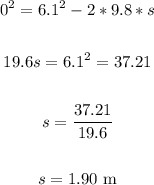
That is the maximum height that the ball reached.