Question

Small cubes with edge lengths of inch will be packed into the right rectangleprism shown. How many small cubes are needed to completely fill the rightrectangular prism?1518157|312ýva -OLolaHin.45oloon-)145585X13ų32In.45font15519وکل

Answer 1

First, calculate if it is possible to cover the 'bottom' of the prism with 1/4in cubes, as shown below

Therefore, to cover the bottom of the prism one needs

`18*18+2*18=18*20=360`

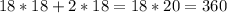
360 cubes.

Now, considering the height of the prism,

`(3.25)/(0.25)=13`

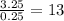
Thus, in total, one requires,

`360*13=4680`

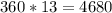
4680 cubes.

The answer is 4680 small cubes