Question

Hi I need help with this question please and thank you

Answer 1

Statement Problem: Given the equation,

`3x^2+5x+3=0`

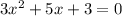
What is the solution(s)?

Solution:

Step 1: Divide through by 3;

`\begin{gathered} (3x^2)/(3)+(5x)/(3)+(3)/(3)=(0)/(3) \\ x^2+(5)/(3)x+1=0 \end{gathered}`

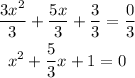
Step 2: Subtract 1 from both sides of the equation,

`\begin{gathered} x^2+(5)/(3)x+1-1=0-1 \\ x^2+(5)/(3)x=-1 \end{gathered}`

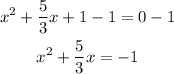
Step 3: Add the square of half of the coeffient of x to both sides of the equation;

`\begin{gathered} x^2+(5)/(3)x+((1)/(2)((5)/(3)))^2=-1+((1)/(2)((5)/(3)))^2 \\ x^2+(5)/(3)x+((5)/(6))^2=-1+((5)/(6))^2 \\ x^2+(5)/(3)x+((5)/(6))^2=-1+(25)/(36) \end{gathered}`

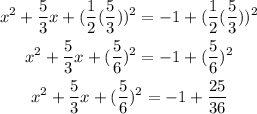
Step 4: Factorize the left side and simplify the right side,

`\begin{gathered} (x+(5)/(6))^2=(-36+25)/(36) \\ (x+(5)/(6))^2=-(11)/(36) \end{gathered}`

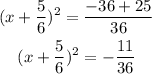
Step 5: Take square root of both sides,

`\begin{gathered} \sqrt[]{(x+(5)/(6))^2}=\sqrt[]{-(11)/(36)} \\ \sqrt[]{(x+(5)/(6))^2}=\frac{\sqrt[]{-11}}{\sqrt[]{36}} \\ x+(5)/(6)=\pm\frac{i\sqrt[]{11}}{6} \end{gathered}`

Step 6: Subtract 5/6 from both sides of the equation,

`\begin{gathered} x+(5)/(6)-(5)/(6)=-(5)/(6)\pm\frac{i\sqrt[]{11}}{6} \\ x=\frac{-5\pm i\sqrt[]{11}}{6} \\ x_1=\frac{-5+i\sqrt[]{11}}{6},x_2=\frac{-5-i\sqrt[]{11}}{6} \end{gathered}`