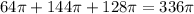Question

Can you please help me out with a question

Answer 1

ok. so the figure is composed by a hemisphere and a cillinder

to find the volume of an hemisphere we use the following formula:

`A_h=2\pi r^2`

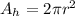
The diameter is 16ft, so the radius is 8ft

`V_h=2\pi(8ft)^2=128\pi ft^2`

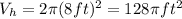
for the cillinder, the volume can be calculated with:

`A_c=h\cdot\pi\cdot\text{diameter}=9ft\cdot\pi\cdot16ft=144\pi`

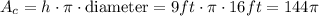
and for last the base of the cilinder has an area of

`A_b=\pi r^2=\pi(8ft)^2=64\pi`

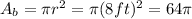
adding all up:

`64\pi+144\pi+128\pi=336\pi`