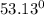SOLUTION
Let us start with the sketch of the figure
Using the trigonometric functions to obtain the measure of the angle.
From the image above,
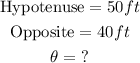
Thus, the trigonometric function that correlates both the opposite and the hypotenuse together is the Sine of angles.
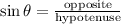
Solving for θ
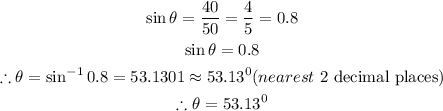
Hence, the measure of the angle the string forms with the ground is