Given the circle shown in the exercise, you can identify that:
![m\angle DEF=(4x+19)\degree]()
By definition:
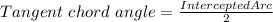
In this case, you know that:
![\begin{gathered} Tangent\text{ }chord\text{ }angle=m\angle DEF=4x+19 \\ \\ InterceptedArc=mDE \end{gathered}]()
The exercise does not provide the measure of the Arc DE, but you know that there are 360 degrees in a circle and you know that the other Arc of the circle is:
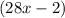
Then, you can set up that:
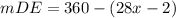
Simplifying, you get that:
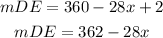
Knowing the expression that represents the Tangent chord angle and the expression that represents the Intercept Arc, you can substitute them into the formula, in order to find the value of "x":
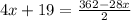
Solving for "x", you get:
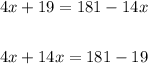

Therefore, the answer is: Option C.