Question

Write an equation of the line in slope-intercept form and in standard form for the line passing through (-1,4) and parallel to x+3y=7

Answer 1

Consider that the equation of a line with slope 'm' and y-intercept 'c' is given by,

`y=mx+c`

Now, the equation of the given line is,

`\begin{gathered} x+3y=7 \\ 3y=-x+7 \\ y=(-1)/(3)x+(7)/(3) \end{gathered}`

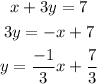
Comparing the coefficients, it is found that the slope of the given line is,

`m=(-1)/(3)`

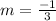
Let the slope of the line which is parallel to this given line be 'n'.

Theorem: Two lines will be parallel if their slopes are equal,

`\begin{gathered} n=m \\ n=(-1)/(3) \end{gathered}`

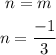
Then the equation of the line will be,

`\begin{gathered} y=nx+c \\ y=(-1)/(3)x+c \end{gathered}`

Given that this parallel line passes through the point (-1,4), so it must satisfy its equation,

`\begin{gathered} 4=(-1)/(3)(-1)+c \\ 4=(1)/(3)+c \\ c=4-(1)/(3) \\ c=(11)/(3) \end{gathered}`

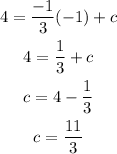
Substitute this value in the equation,

`y=(-1)/(3)x+(11)/(3)`

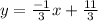
Thus, the equation of the line passing through (-1,4) and parallel to x+3y=7 is obtained as,

`y=(-1)/(3)x+(11)/(3)`

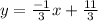
the slope