We will solve as follows:
*We will use the following expressions:
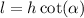
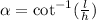
[Thit these we will find the angle on the ground and using this we will determine x]
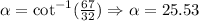
So, we have that the other angle is 25.53. Now, since we know that the sum of all internal angles of a triangle adds 360°, and we already have two sides, we find the value of x as follows:
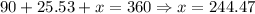
So, the angle of x is approximately 244°.