Question

Please help! Can anyone help me out with this question?

Answer 1

`\displaystyle h'(s) = 64s + 20`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Distributive Property

Algebra I

• Terms/Coefficients

Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Product Rule]:
`\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)`

Explanation:

Step 1: Define

`\displaystyle h(s) = (-8s - 9)(-4s + 2)`

Step 2: Differentiate

1. [Derivative] Product Rule:
   `\displaystyle h'(s) = (d)/(ds)[(-8s - 9)](-4s + 2) + (-8s - 9)(d)/(ds)[(-4s + 2)]`
2. [Derivative] Basic Power Rule:
   `\displaystyle h'(s) = (1 \cdot -8s^(1 - 1) - 0)(-4s + 2) + (-8s - 9)(1 \cdot -4s^(1 - 1) - 0)`
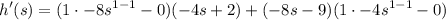
3. [Derivative] Simplify:
   `\displaystyle h'(s) = (-8)(-4s + 2) + (-8s - 9)(-4)`
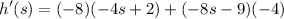
4. [Derivative] Distribute [Distributive Property]:
   `\displaystyle h'(s) = 32s - 16 + 32s + 36`
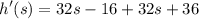
5. [Derivative] Combine like terms:
   `\displaystyle h'(s) = 64s + 20`

Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Derivatives

Book: College Calculus 10e