Question

When comparing the f(x) = x2 + 2x and g(x) = log(2x + 1), on which interval are both functions negative?A. (–∞, –2)B. (–2, 0)C. (–1, 1)D. (∞, ∞)

Answer 1

Given the functions:

`f(x)=x^2+2x`
`g(x)=log(2x+1)`

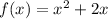
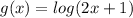
You can graph both functions. See the graph shown below:

You know that the negative numbers are less than zero. Therefore, in order to determine the interval on which both functions are negative, you can use the graph:

The red lines show the interval. This is:

`(-2,0)`

Hence, the answer is: Second option.