Question

If there are 40 boxes with the following dimensions and the stacking height is four, what floor space is needed to store the boxes? length = 3 feet, width = 4 feet, and height =5 feet96 square feet100 square feet120 square feet150 square feetNone of these choices are correct.

Answer 1

There are 40 boxes with a stacking height of 4. This means that four boxes are stacked together.

How many numbers of a stack of 4 boxes will equal 40 boxes

To get that we have

`\begin{gathered} numberofstack=\frac{Total\text{ number of boxes}}{number\text{ of boxes in a stack}} \\ =(40)/(4)=10\text{ stacks} \end{gathered}`

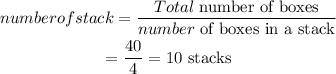
To get the floor space area, we need to find the base area of each box

Given the dimensions of the box as length=3feet; width =4feet and height = 5feet

The base of a box a rectangle shape

To find the area of a box, we find the base area which is the area of a rectangle using the length and the width

`\begin{gathered} the\text{ base area=length }* width \\ \text{length}=3ft;\text{ width=4ft} \\ \text{area}=3ft*4ft \\ =12ft^2 \end{gathered}`

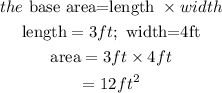
We have 10 boxes occupying the floor space. so to calculate the area of the floor space we multiply the area of the base by 10

`\begin{gathered} \text{Area of the floor space=10}* area\text{ of each of the box } \\ =10*12ft^2 \\ =120ft^2 \end{gathered}`

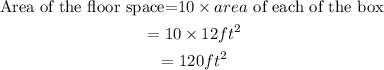
Hence the floor space needed to store the boxes is 120 square feet