Okay, here we have this:
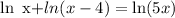
Applying the properties of logarithms we obtain:
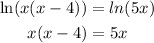
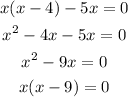
This mean that:
x=0 or x-9=0
x=0 or x=9
We are going to verify which of the solutions works:
x=0:
ln(0)+ln(0-4)=ln(5*0)
ln(0)+ln(-4)=ln(0)
ln(0*-4)=ln(0)
ln(0)=ln(0)
As ln(0)=undefined, the solution x = 0 is false. Let's check the other one: x=9:
ln(9)+ln(9-4)=ln(5*9)
ln(9)+ln(5)=ln(45)
ln(5*9)=ln(45)
ln(45)=ln(45)
This solution satisfies equality, therefore the solution of the equation is x=9.