Question

You roll a 6-sided die.What is P(3)?.Write your answer as a fraction or whole number,

Answer 1

If the six-sided die is numbered from 1 to 6 and considered that it is balanced, this means that all values are equally probable. To determine this probability you have to calculate the quotient between the number of favorable outcomes and the total number of outcomes.

For the event "rolling a 3", the number of favorable outcomes is equal to the times that number "3" is labeled on the faces of the die, in this case, there is only one face labeled 3. So the number of favorable outcomes is 1.

The total number of outcomes corresponds to the number of faces of the die, in this case, there are 6 faces on the die so there are 6 possible outcomes.

Then you can calculate the probability of rolling a 3 as follows:

`\begin{gathered} P(3)=\frac{nº\text{favorable outcomes}}{total\text{ outcomes}} \\ P(3)=(1)/(6) \end{gathered}`

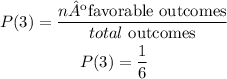
The probability of rolling a three is 1/6