Given the function
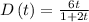
Notice that

Then, integrate D(t) from t=0 to t=3, as shown below
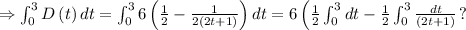
Then,
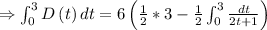
As for the remaining integral, set x=2t+1; then dx=2dt. Solving using that substitution,
as for the integration limits, when t=3, x=7, and when t=0, x=1.
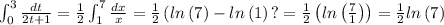
Therefore,
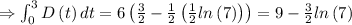
Rounding to three decimal places,
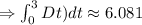
Thus, the answer is 6.081