Question

Find the real and/or complex solutions. X^2-12x= -27

Answer 1

Consider the following equation:

`x^2-12x=-27`

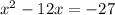
this is equivalent to the following quadratic equation:

`x^2-12x+27=0`

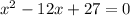
to solve this quadratic equation, we can apply the following quadratic formula:

`x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

here,

a = 1

b = -12

and

c = 27

so that, the solutions to the given quadratic equation are:

`x_1\text{ = }\frac{12+\sqrt[]{(-12)^2-4(1)(27)}}{2(1)}=\frac{12+\sqrt[]{36}}{2}=(12+6)/(2)=9`

and

`x_2\text{ = }\frac{12-\sqrt[]{(-12)^2-4(1)(27)}}{2(1)}\text{ =}\frac{12-\sqrt[]{36}}{2}\text{= }(12-6)/(2)=3`

So that, the correct answer is:

the solutions are:

9 and 3.