Answer:
The volume of a cone is calculated using the formula below
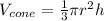
The height is multiplied by 4, we will have the new height be
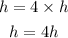
The radius id multiplied by 4, we will have the new radius be
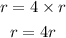
By substituting the new values of the height and radius in the equation od the volume of a cone, we will have
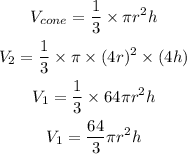
By dividing the new volume by the initial volume, we will have
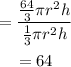
Hence,
The final answer is
The volume of the cone is multiplied by 64