Question

In the reaction CO (g) + H2O (g) <=> CO2 (g) + H2 (g), Kc = 23.2 at 600K. If we introduce 0.250 mol of CO and 0.250 mol of H2O, how many moles of CH2 and H2 will be present once equilibrium is reached?

Answer 1

No volume information is given, therefore, we will assume a volume of 1L to proceed with the calculations, in other words, all calculations will be per liter of solution.

Now, we have the balanced reaction:

CO (g) + H2O (g) <=> CO2 (g) + H2 (g)

We are told that the initial moles of the reactants are 0.250 mol for CO and 0.250 mol H2O, as the ratio is one to one, we can then say that the moles of each product will react equally and their concentration will be the same between them throughout the process. The moles that react before reaching the equilibrium will denominate them with the letter x.

Now, we have the initial moles of the reactants. The moles of the products will be equal to the moles that react.

Initial Concentration (reactants): 0.250 mol/L

Equilibrium concentration (Products): x mol/L

Final concentration (Reactants): 0.250-x mol/L

Equilibrium constant will be:

`K\text{ = 23.2 = }(\lbrack x\rbrack\lbrack x\rbrack)/(\lbrack0.250-x\rbrack\lbrack0.250-x\rbrack)`
`23.2\text{ = }(\lbrack x\rbrack^2)/(\lbrack0.250-x\rbrack^2)`

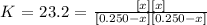
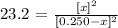
`\sqrt[]{23.2}=\text{ }(\lbrack x\rbrack)/(\lbrack0.250-x\rbrack)`

Now, we clear x

`\begin{gathered} 4.82\text{ = }(\lbrack x\rbrack)/(\lbrack0.250-x\rbrack) \\ 4.82\text{ x 0.250 = x(1+4.82)} \\ x=\frac{\text{ 4.82 x 0.250}}{1+4.82} \\ x\text{ = 0.207 mol} \end{gathered}`

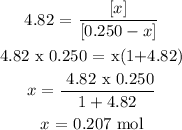
So, once will be equilibrium is reached will be present 0.207 mol of CH2 and H2