Question

mr. Krabs saw some rickety chairs on sale they were 89.5% off the normal price was $15 each mr. crab four chairs how much did he spend

Answer 1

The normal price of each chair is

`=\text{ \$15}`

The percentage off the normal price is

`=89.5\text{ \%}`

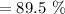
The percentage of the present price of each chair will be

`\begin{gathered} 100\text{ \% - 89.5 \%} \\ =10.5\text{ \%} \end{gathered}`

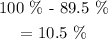
To calculate the present value of one chair, we will use the formula below

`=\text{percentag of the normal price}* normal\text{ price}`

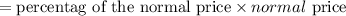
By substituting the values, we will have

`\begin{gathered} \text{new price of each chair will be=}(10.5)/(100)*15 \\ \text{new price of each chair will be}=(157.5)/(100) \\ \text{new price of each chair will be}=\text{ \$1.575} \end{gathered}`

Since Mr .Krabs bought 4 chairs, the amount he spent will be

`\text{Amount spent = price of each chair}* Number\text{ of chairs}`

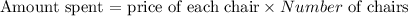
By substituting the values, we will have

`\begin{gathered} \text{Amount spent = price of each chair}* Number\text{ of chairs} \\ \text{Amount spent}=1.575*4 \\ \text{Amount spent}=\text{ \$6.30} \end{gathered}`

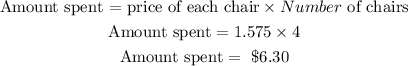
Therefore,

The amount Mr.Krabs spent is = $6.30