To solve the exercise, we can first find the equation of the line f(x). To do this, we can first take two points through which the line passes and find its slope using this formula:
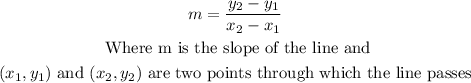
In this case, we have:
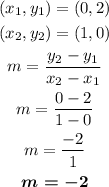
Now we can use the point-slope formula to find the equation of the line f(x):
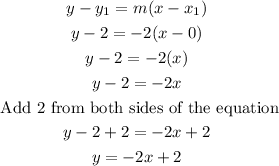
Then, the equation of the line f(x) is:
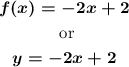
To find the inverse function, g(x), we swap x and y in the equation of the line f(x), solve for y and, we rewrite y as g(x):

Then, the equation of the line g(x) is:
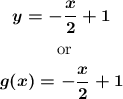
Finally, to complete the table, we can plug the given ordered pair into the equation of the line g(x) and see if the equation is satisfied:
• Ordered pair (-3,4)
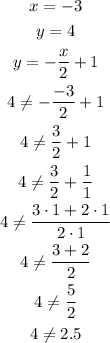
Since 4 is different from 2.5, the ordered pair does not satisfy the equation and therefore is not part of g(x).
• Ordered pair (-2,2)
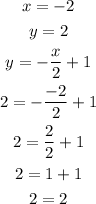
As it is true that 2 is equal to 2, the ordered pair satisfies the equation and, therefore, is part of g(x).
• Ordered pair (4,-1)
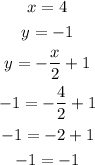
As it is true that -1 is equal to -1, the ordered pair satisfies the equation and, therefore, is part of g(x).
Therefore, the complete table is
You can see the above in the graph shown below: