Question

O GRAPHS AND FUNCTIONSFinding slopes of lines parallel and perpendicular to a line given.

Answer 1

Step 1: Concept

`\begin{gathered} \text{Two lines are perpendicular if the product of their slopes }=\text{ -1} \\ m_1\text{ }* m_2\text{ = -1} \end{gathered}`

`\begin{gathered} \text{Two lines are parallel if their slopes are equal} \\ m_1=m_2 \end{gathered}`

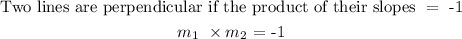
Step 2:

Write the equation of the line in the form of y = mx + c, where m is the slope.

`\begin{gathered} -5x\text{ - 7y = -8} \\ -5x\text{ + 8 = 7y} \\ 7y\text{ = -5x + 8} \\ y\text{ = -}(5)/(7)x\text{ + }(8)/(7) \end{gathered}`

`\text{Therefore, the slope of the line m}_1\text{ = -}(5)/(7)`

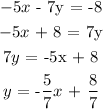
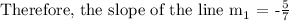
Step 3

To find the slope of a line perpendicular to the line with slope -5/7 can be found using the formula below

`\begin{gathered} m_1\text{ }* m_2\text{ = -1} \\ -(5)/(7)\text{ }* m_2\text{ = -1} \\ -5m_2\text{ = -7} \\ m_2\text{ = }(-7)/(-5) \\ m_2\text{ = }(7)/(5) \end{gathered}`

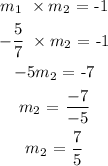
Step 4:

To find the slope of a line parallel to the line with slope -5/7 can be found using the formula below.

`\begin{gathered} m_1=m_2 \\ m_2\text{ = -}(5)/(7) \end{gathered}`

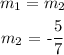
Final answer

`\begin{gathered} \text{Slope of a perpendicular line = }(7)/(5) \\ \\ \text{Slope of parallel line = -}(5)/(7) \end{gathered}`