Question

Find so that the point (-1,2) is on the graph f(x)=ax^2+4. What does A equal?

Answer 1

We have to find the parameter a so that (-1,2) is part of the function f(x) = ax²+4.

To check if a point is part of a function, we can replace the values of x and y = f(x) with the coordinates of the point and then, if the equation stays true, then the point is part of the function.

So for (x,y) = (-1,2) to be part of the function y = f(x), this equation has to stands true:

`\begin{gathered} y=f(x) \\ y=ax^2+4 \\ 2=a(-1)^2+4 \\ 2=a+4 \\ a=2-4 \\ a=-2 \end{gathered}`

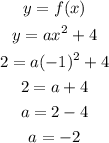
Then, the function would have to be f(x) = -2x² + 4.

We can check with a graph as:

Answer: a = -2