Let 'x' be the amount invested at 11% interest and let 'y' be the amount invested at 9%. Then, since Sang investedn $191 more than 5 times the amount 'y' at 9%, we have:
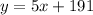
Also, since the total interest is the sum of the interest of both accounts, we have the following equation:
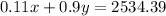
if we substitute the first equation on the second, we get the following:
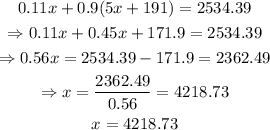
now that we know the amount y, we can use it to find the amount y:
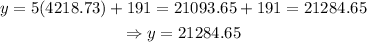
therefore, Sang invested $4218.73 at 11% interest and $21,284.64 at 9% interest