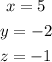1 Answer

Usman Iqbal · Answer 1 · 2023-04-03T21:27:11+0000

For the system of equation:

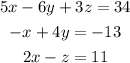
$\begin{gathered} 5x-6y+3z=34 \\ -x+4y=-13 \\ 2x-z=11 \end{gathered}$

To solve by elimination, we need to eliminate variables by adding equations.

The last two equations have x and z with -1 as coefficeint, so it is easy to use them to eliminate variables.

Since x appears in both, but z only in the last, let's eliminate z first.

To eliminate it from the first equation, we need to add the last equation multiplied by 3:

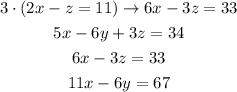
$\begin{gathered} 3\cdot(2x-z=11)\to6x-3z=33 \\ 5x-6y+3z=34 \\ 6x-3z=33 \\ 11x-6y=67 \end{gathered}$

Now, to eliminate x from it, we substract the second equation multiplied by 11:

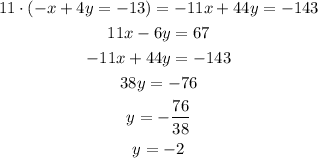
$\begin{gathered} 11\cdot(-x+4y=-13)=-11x+44y=-143 \\ 11x-6y=67 \\ -11x+44y=-143 \\ 38y=-76 \\ y=-(76)/(38) \\ y=-2 \end{gathered}$

Now, we can use this y value into the equation with only x and y:

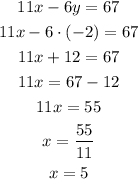
$\begin{gathered} 11x-6y=67 \\ 11x-6\cdot(-2)=67 \\ 11x+12=67 \\ 11x=67-12 \\ 11x=55 \\ x=(55)/(11) \\ x=5 \end{gathered}$

And now, we can substitute this value into the equation with only x and z:

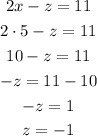
$\begin{gathered} 2x-z=11 \\ 2\cdot5-z=11 \\ 10-z=11 \\ -z=11-10 \\ -z=1 \\ z=-1 \end{gathered}$

So, the solution is:

$\begin{gathered} x=5 \\ y=-2 \\ z=-1 \end{gathered}$

Please log in or register to add a comment.